What is a Fibonacci Heap?
A fibonacci heap is a data structure that consists of a collection of trees which follow min heap or max heap property. The trees are constructed in a way such that a tree of order n has at least Fn+2 nodes in it, where Fn+2 is the (n + 2)th Fibonacci number.
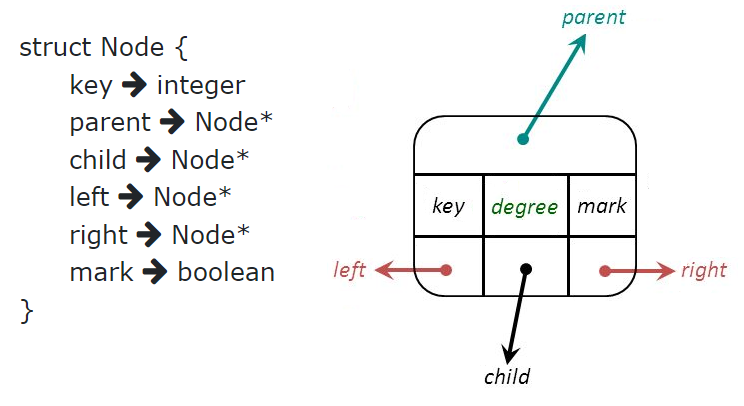
Node structure
Operations on a Fibonacci Heap
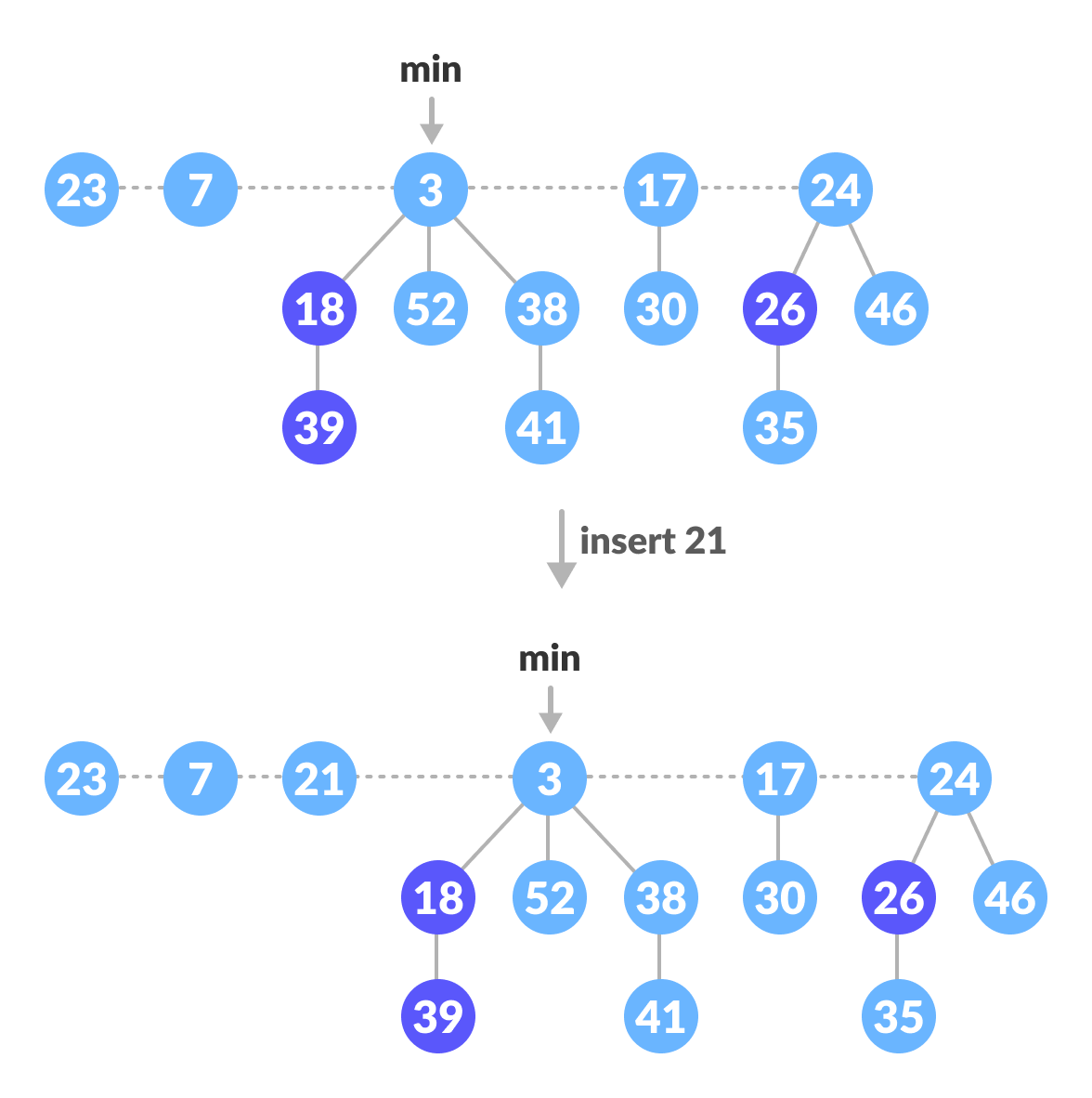
Insertion Algorithm
- Create a new node for the element
- Check if the heap is empty
- If the heap is empty, set the new node as a root node and mark it min
- Else, insert the node into the root list and update min
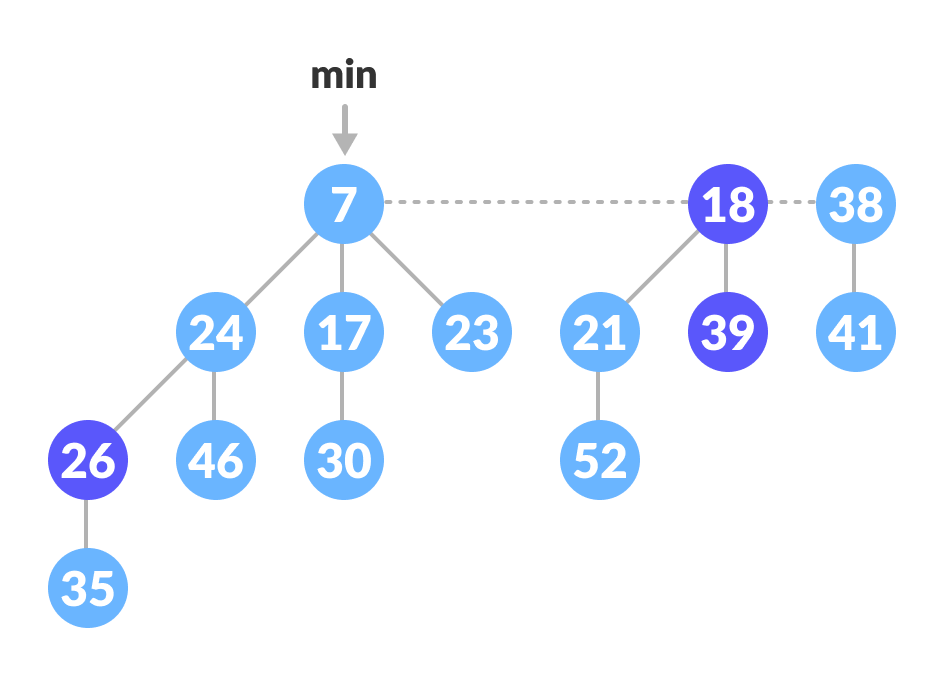
Find Min
The minimum element is always given by the min pointer
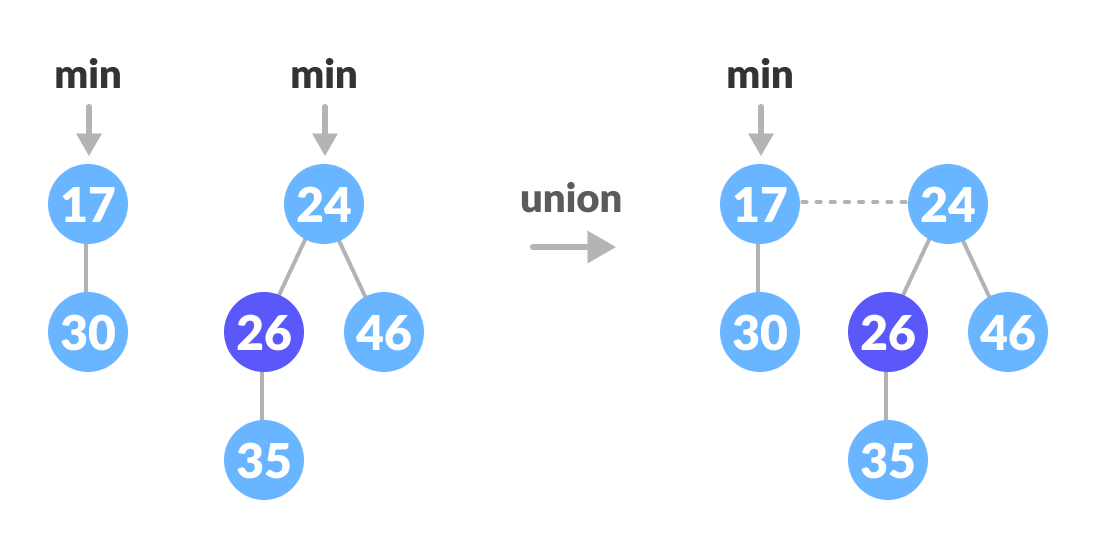
Union
- Concatenate the roots of both the heaps
- Update min by selecting a minimum key from the new root lists
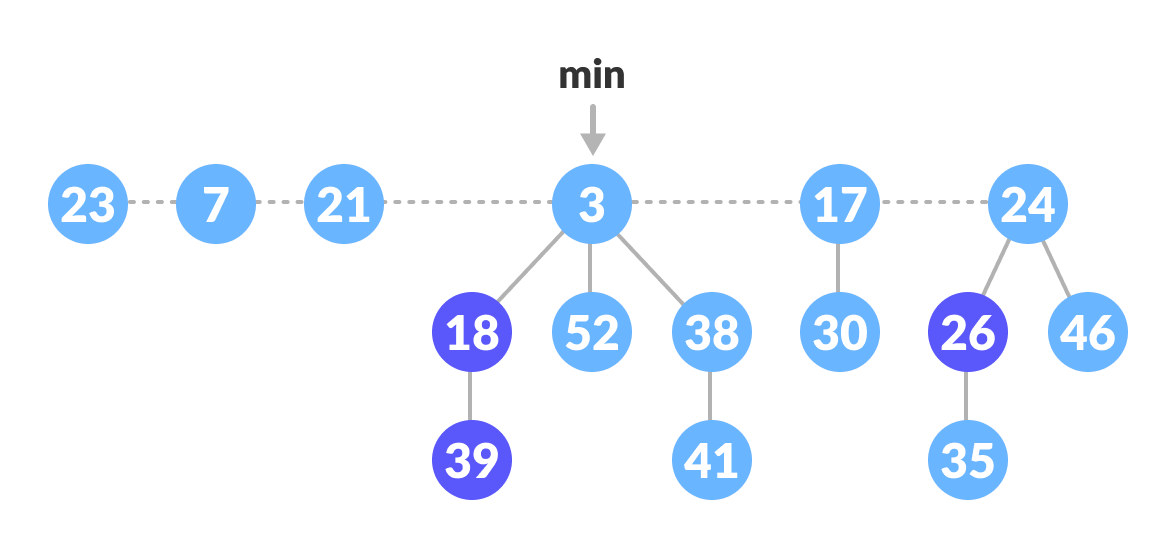
Extract Min
The node with minimum value is removed from the heap and the tree is re-adjusted
- Delete the min node
- Set the min-pointer to the next root in the root list
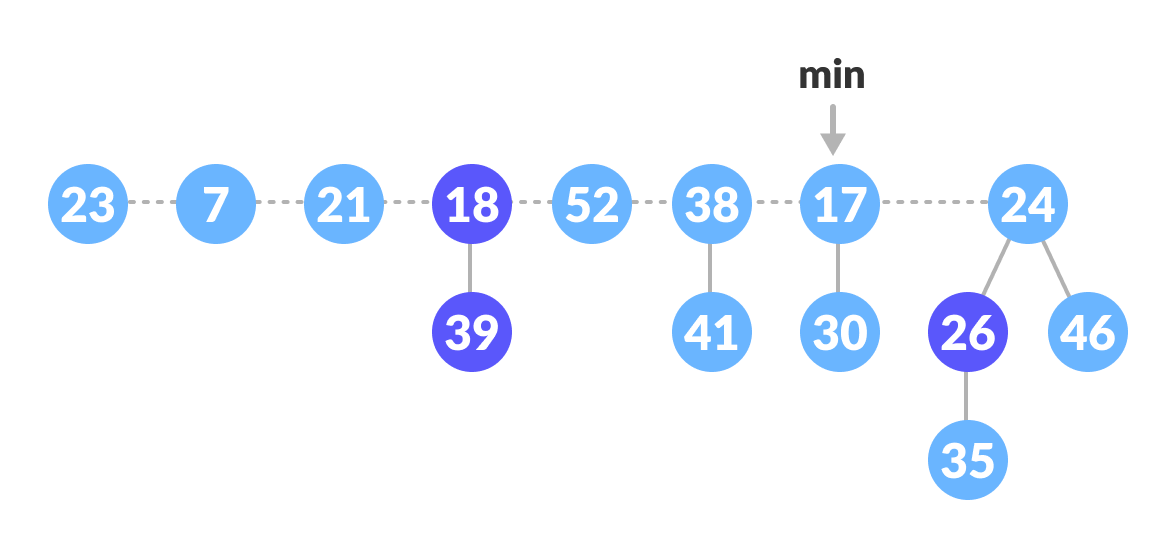
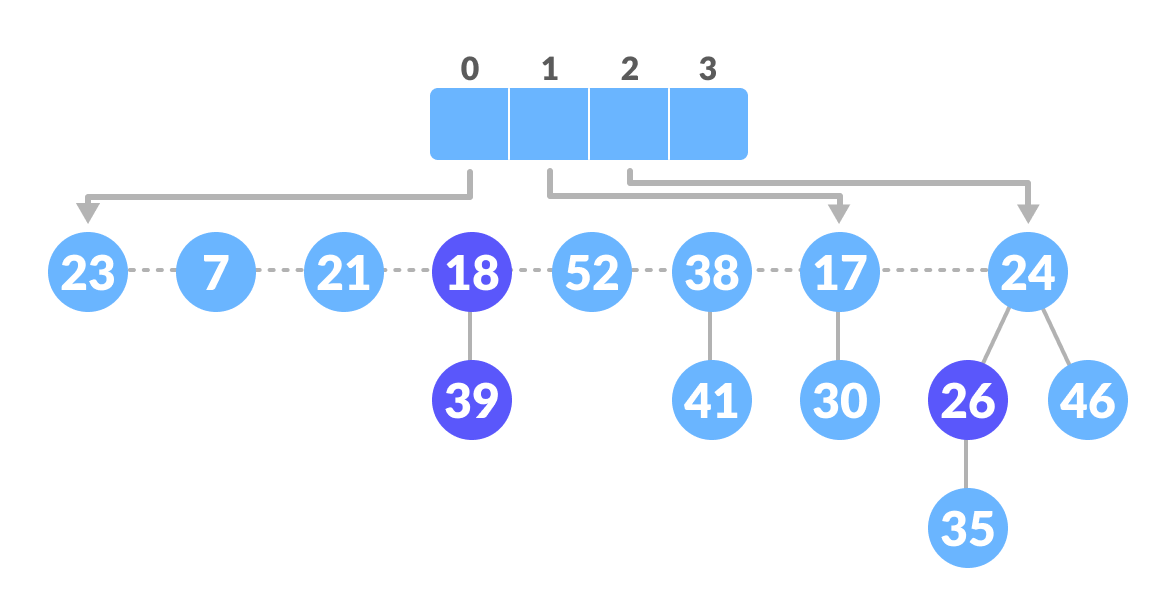
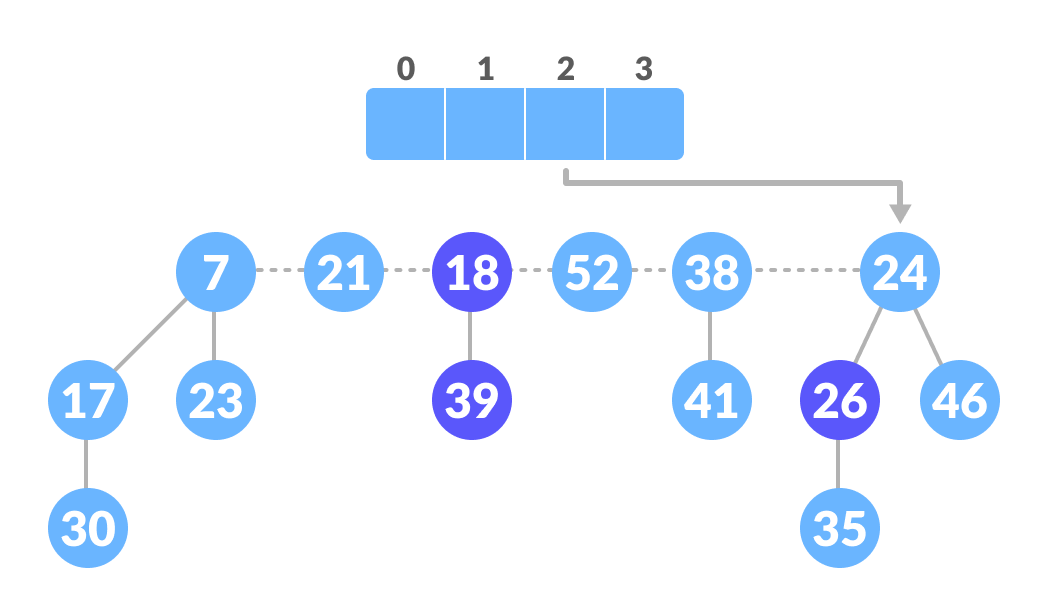
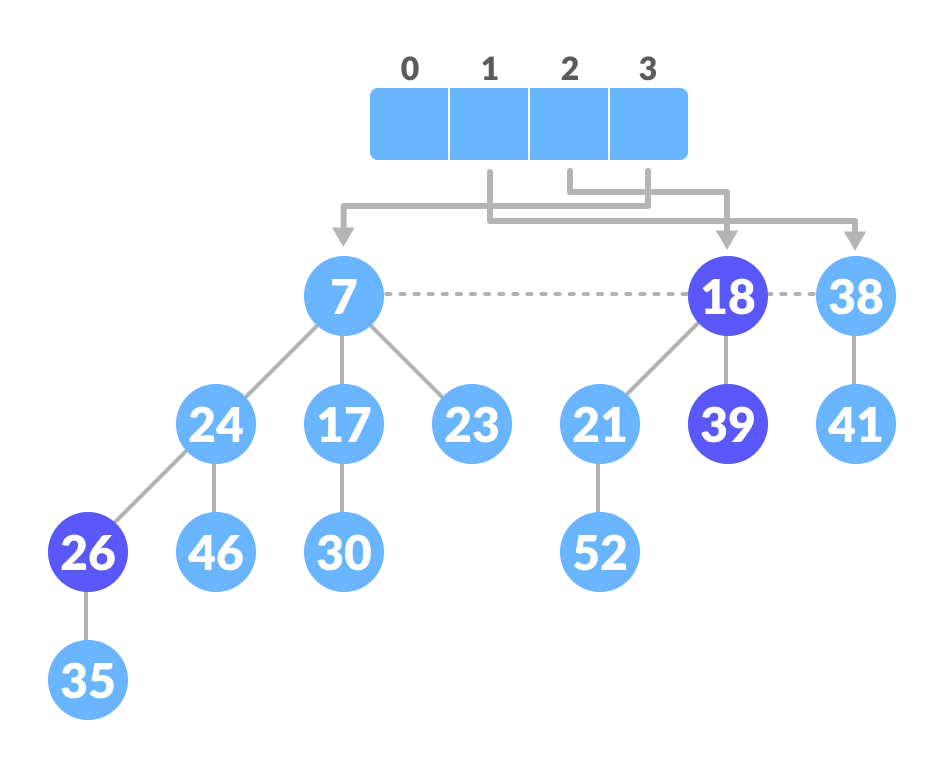
- Create an array of size equal to the maximum degree of the trees in the heap before deletion
- Repeat until there are no multiple roots with the same degree
- Map the degree of current root (min-pointer) to the degree in the array
- Map the degree of next root to the degree in array
- If there are more than two mappings for the same degree, then apply union operation to those roots such that the min-heap property is maintained (i.e. the minimum is at the root)
 |
 |
 |
 |
 |
 |
 |
 |
 |