SCAN (Elevator Algorithm)
Scan is often called Elevator Scheduling Algorithm, due to the way it works.
In SCAN, disk arm starts from one end of the disk and executes all the requests in its way till it reaches the
other end.
As soon as it reaches the other end, it reverses its direction, hence it moves back and forth
continuously (like an elevator) to access the disk.
Advantages:
- There is no starvation.
- Average Response time, and its variance is low.
- High throughput.
- Simple to understand and better in performance compared to FCFS
Disadvantages:
- Its Implementation can be difficult and complex.
- The requests at the midrange are serviced more and those arriving behind the disk arm will have to wait. Thus, fair chance is not given to each request.
- Arm will move to end even when there is no request to execute.
Example:
-
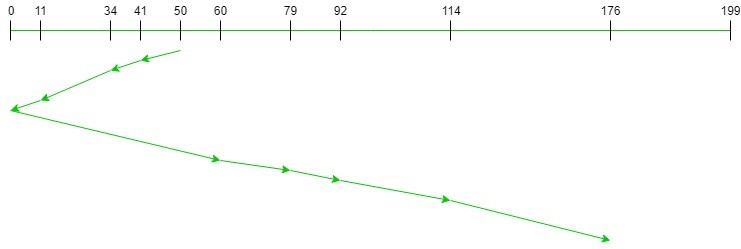
Consider a disk containing 200 tracks (0-199) and the request queue includes the track number 176, 79, 34, 60,
92, 11, 41, 114 respectively.
The current position of read//write head is 50, and direction is towards the larger value. - Calculate the total number of cylinders moved by the head using SCAN disk scheduling.
- As mentioned in the following example, the disk contains 200 tracks. So, we take a track line between 0 to 199.
-
The current position of the read/write head is 50. So, we start at 50, then move the read/write head.
When all the requests are addressed, then we calculate a total number of cylinders moved by the head. -
Total Number of cylinders moved by head
= (50-41)+(41-34)+(34-11) +(11-0)+(60-0)+(79-60) +(92-79)+(114-92)+(176-114)
= 226
Steps to Implement Algorithm:
- Let Request array represents an array storing indexes of tracks that have been requested in ascending order of their time of arrival. 'head' is the position of disk head.
- Let direction represents whether the head is moving towards left or right.
- In the direction in which head is moving service all tracks one by one.
- Calculate the absolute distance of the track from the head.
- Increment the total seek count with this distance.
- Currently serviced track position now becomes the new head position.
- Go to step 3 until we reach at one of the ends of the disk.
- If we reach at the end of the disk reverse the direction and go to step 2 until all tracks in request array have not been serviced.
Time Complexity: O ( N * logN ) Auxiliary Space: O ( N )
Simulate